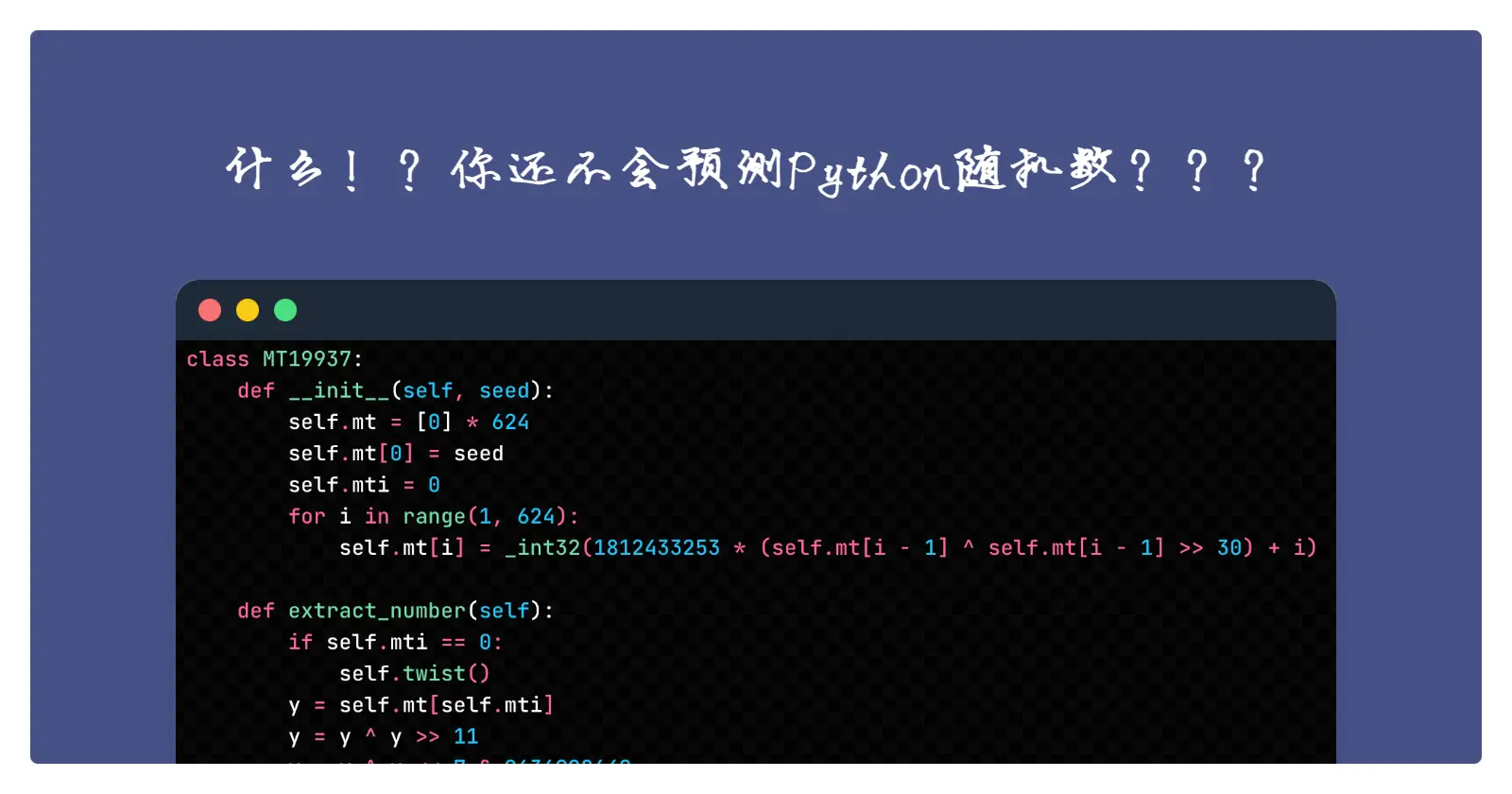
Python随机数的背后：MT19937算法之——小试牛刀

本文为几道 MT19937 预测题的题解。这些题都非常基础 + 典型，十分适合入门。

本文用到的 mt19937 来自此 gist。

第一题

python

#!/usr/bin/env python3

import random

for _ in range(624):
    print(random.getrandbits(32))

if input() == str(random.random())
    print(open("flag").read())

非常简单的预测，给了连续 624 个 32bit 随机数，只需把它们依次输入预测器，就能恢复出完整的内部状态。

python

import tqdm
from mt19937 import MT19937Predictor
from pwn import remote

r = remote(HOST, PORT)
predictor = MT19937Predictor()
for _ in tqdm.tqdm(range(624)):
    data = int(r.recvline().decode())
    predictor.setrand_int32(data)

r.sendline(str(predictor.random()).encode())
print(r.recv().decode())

第二题

python

#!/usr/bin/env python3

import random

number = random.getrandbits(32)

for _ in range(624):
    print(random.getrandbits(32))

if input() == str(number):
    print(open("flag").read())

同样先通过连续的 624 个 32bit 随机数恢复出内部状态，然后我们往回倒 625 次迭代，即可恢复出最前面的那个随机数产生之前的状态。

python

import tqdm
from pwn import remote
from mt19937 import MT19937Predictor

r = remote(HOST, PORT)
predictor = MT19937Predictor()
for _ in tqdm.tqdm(range(624)):
    data = int(r.recvline().decode())
    predictor.setrand_int32(data)

for i in range(625):
    predictor.unextract_number()

ans = predictor.getrandbits(32)
r.sendline(str(ans).encode())
print(r.recv().decode())

第三题

python

#!/usr/bin/env python3

import random

for _ in range(19938):
    print(random.getrandbits(1))

if input() == str(random.getrandbits(64)):
    print(open("flag").read())

这一题就稍微难一些了，虽然看上去是连续生成了 19938 个 bit，但因为这个算法最小的生成单位是 32bit，每次调用 getrandbits(1) 时，其实内部先会生成一个 32bit 的随机数，然后取其最高位返回。不过经过前面的一些分析，我们很容易发现一个关键点：即 MT19937 算法每次迭代产生的随机数的每一个 bit，其实都是它内部状态某些 bit 的异或得来的，这说明取出随机数的操作是一个 $G F (2)$ 上的线性运算，如果我们拿到了 19937 个 bit，即使它们是不连续的，只要我们能够分析出一些前后 bit 的对应关系，便可以通过求解线性方程组来解出状态。解方程神器自然少不了 z3，我也找到了一个利用 z3 来恢复 MT19937 内部状态的项目：SymRandCracker

可惜，这道题的已知 bit 过于分散，每 32 个 bit 才知道其中一个的值，如果全输入符号求解器，复杂度会拉满，不过好在我们知道每次给的 bit 的位置（MSB）。

我们设初始状态下 random 的状态向量为 $\vec{a}$ ，则 $\vec{a}$ 相当于一个 $624 \times 32 = 19968$ 维的向量。再假设此状态下连续生成的 624 个 32bit（一共也是 19968 个 bit）组合成的向量为 $\vec{b}$ ，则存在一个 $19968 \times 19968$ 的矩阵 $M_{1}$ 满足：

M_{1} \vec{a} = \vec{b} (\mod 2)

不妨大胆一点，假设从内部状态 $\vec{a}$ 开始连续生成的 19938 个 32bit 的 MSB（一共 19938 个 bit）组合成的向量为 $\vec{c}$ ，是否存在一个 $19938 \times 19968$ 的矩阵 $M_{2}$ 满足：

M_{2} \vec{a} = \vec{c} (\mod 2) ?

答案是肯定的。

并且我们还能在本地预生成好这个矩阵，然后从服务器拿到 19938 个 MSB（ $\vec{c}$ ）后直接解出随机数发生器最开始的内部状态 $\vec{a}$ 。

这里使用 Sage 编写代码：

python

import random
import tqdm
import os

length = 624 * 32
def generate_state():
    state = [int(0)]*624
    i = 0
    while i<length:
        idx = i//32
        expont = i%32
        state[idx] = int(1<<(31-expont))
        s = (3,tuple(state+[int(624)]),None)
        yield s
        state[idx] = int(0)
        i += 1

        
def get_row():
    gs = generate_state()
    for i in range(length):
        s = next(gs)
        random.setstate(s)
        row = vector(GF(2), [random.getrandbits(1) for j in range(length)])
        yield row


def build_matrix():
    b = matrix(GF(2),length,length)
    rg = get_row()
    for i in tqdm.tqdm(range(length)):
        b[i] = next(rg)
    return b


if not os.path.exists('Matrix.sobj'):
    b = build_matrix()
    b.save("Matrix.sobj")

思路是遍历所有仅一个 bit 为 1，其他 bit 为 0 的状态（共 19968 个），每次将此状态赋值给随机数发生器，然后让它根据此状态连续生成 19968 个 32bit，我们每 32 个 bit 取出其 MSB，组合为矩阵的一行。将每个状态对应的行拼起来，组合得到一个 $19968 \times 19968$ 的矩阵。由于这个生成过程长达 20 分钟，故一次生成结束就存在本地，方便后面直接读取。

求解时由于我们只有 19938 个输入，就将矩阵进行一个截断：

python

T = load('Matrix')
T = T[:, :19938]

读入服务器发来的数据，然后调用 Sage 的 solve_left，解一下方程即可：

python

from pwn import remote

r = remote(HOST, PORT)

leak = [int(r.recvline().strip().decode()) for i in tqdm.tqdm(range(19938))]
leak = vector(GF(2), leak)
x = T.solve_left(leak)
x = ''.join([str(i) for i in x])
state = []
for i in range(624):
    tmp = int(x[i * 32:(i + 1) * 32], 2)
    state.append(tmp)

random.setstate((3, tuple(state + [624]), None))
for i in range(19938):
    random.getrandbits(1)

r.sendline(str(random.getrandbits(64)).encode())
r.recv()