手搓神经网络系列之——计算图及其构建方式的选择

此文将简单介绍神经网络在编程实现中最重要的概念之一 —— 计算图（Computation Graph）。

其实这部分的内容网上很多博客已经说的很清楚了，那我为什么还要写呢？当然为了凑篇水文！（没看到本站其他文章都是类似于这样的水文吗）除此以外，本文还将介绍计算图的两种常见的构建方式，以及我在自己的神经网络框架中，选择了哪一种作为计算图的实现。

本系列全部代码见下面仓库：

autograd-with-numpy

GitHub

如有算法或实现方式上的问题，请各位大佬轻喷 + 指正！

在进入正文前，首先请确保你知道训练神经网络的最流行的算法是所谓的 “误差逆传播（Error BackPropagation）算法”，我则习惯于称之为 “反向传播”，或 backward。若你还不知道反向传播，你可能没办法理解计算图是为了干啥。

计算图

下面贴一条 Google 上搜到的对计算图的定义：

计算图被定义为有向图，其中节点对应于数学运算。 计算图是表达和评估数学表达式的一种方式。

我再补充一点，即在有向的意义上，计算图是无环的。

这个定义感觉啥也没说，还是先举一个例子看看吧：

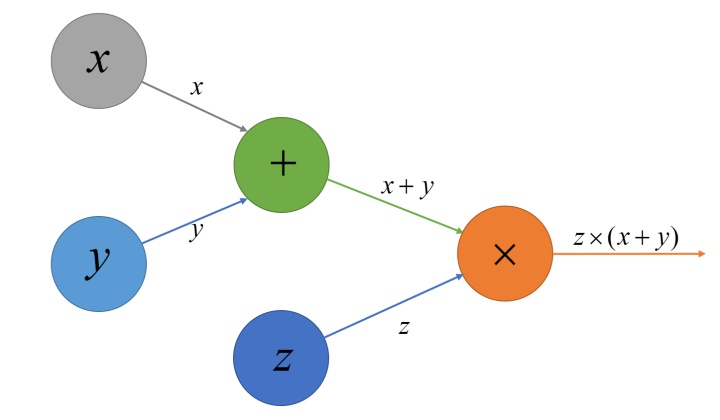
对于这样一个计算式： $e = z \times (x + y)$ ，我们可以构造以下计算图：

对比计算式和计算图，容易猜到计算图的构造方法：若有两个数，或者更一般地，N 个数（N≥1），通过某种运算得到另一个数，那么在计算图中，我们就在这 N 个数所在的节点上各引出一条箭头，指向运算得到的结果，同时在运算结果的节点上，记录下运算符号。

在上面这个图中，有唯一的输出元素，称为 “根”，若不考虑 $z \times (x + y)$ 可能继续参与的之后的运算，那么这个计算图的 “根” 即是 $z \times (x + y)$ ，或 $e$ 所在的节点。不由任何其他数运算得来的数称为图上的 “叶子”，在此例里，“叶子” 有三个： $x, y, z$ 所在的节点，这是因为它们并不是通过其他数字运算得到的，换句话说，没有任何节点指向它们。

有一点需要说明一下，上面的定义里提到，节点对应于数学运算，但个人认为，其实每个节点可以把运算的结果存储进去，这个是后面写代码时需要考虑的事情。

由一些数通过运算得来的数，若其不是 “根”，我把它称为 “中间结果”，在上面的例子里，加号所在节点表示的数 $(x + y)$ 是一个 “中间结果”，但其实 “中间结果” 和 “根” 在本质上好像没什么区别，唯一区别就是到了 “根” 这个位置，图终止了。

上面这个例子里的运算式非常的简单，但即使在复杂的神经网络中，最终的损失（Loss）也是通过一系列的上面这样简单的运算得到的，因此完全可以类似地构造一个计算图（当然神经网络的计算图可能会复杂到不能看，故这里不再举例子，此链接给出了一个仅仅只有二层的 LSTM 的计算图，诸位可以细品一下），计算图可以完全表达出神经网络的结构与运算顺序，因此在神经网络中至关重要。

相信看到这里，聪明的你肯定看明白了计算图的构造过程，接下来，就涉及到神经网络的训练方法 —— 误差逆传播算法。

误差逆传播算法

类似于一些简单的机器学习模型，神经网络这种庞然大物也通过梯度下降进行训练，所谓梯度下降，就类似于水往低处流，把训练时计算得到的误差看成是对神经网络中所有参数的函数，将误差对所有参数求梯度，然后让每个参数沿着其梯度方向进行更新迭代，在适当的步长下，就能让误差收敛于极小值点。

对于简单的函数，我们通过纸笔甚至心算就能算出其对每个变量的梯度，但神经网络结构复杂，算梯度的事还是交给计算机来完成吧。神经网络的著名算法 “误差逆传播” 就是用来解决这个事的。

误差逆传播是指一种神经网络模型对它的每一个需要计算梯度的参数计算梯度的最常用的算法。

我们继续回顾前面一个简单的例子，现在假设有一个简单到离谱的神经网络，只有两个参数 $y, z$ ，而且其 Loss 的计算过程恰好就是 $e = z \times (x + y)$ ，这里假设 $x$ 是一个常数，姑且理解为训练数据好了 hhh，它相当于一个不需要计算梯度的 “叶子”。那么我们就需要分别计算 $e$ 对 $y$ 和 $z$ 的梯度。

通过简单的链式法则易知：

\begin{aligned} \frac{\partial e}{\partial y} & = \frac{\partial e}{\partial (x + y)} \frac{\partial (x + y)}{\partial y} \\ = z \times 1 = z \\ \frac{\partial e}{\partial z} = x + y \end{aligned}

注意上面第一个式子，细心的朋友可就发现了 $e$ 对 “叶子” 节点 $y$ 的梯度恰好相当于 $e$ 对 “中间结果” $(x + y)$ 的梯度与 $(x + y)$ 对 $y$ 的梯度的乘积，相当于如果我们已经得到了误差对某个中间结果的梯度，就可以将这个对中间结果的梯度用于更前向的梯度计算中，而不用从头开始重新算一遍。这也是误差逆传播名称的由来，这误差看上去就是逆着计算图的箭头从 “根” 流向 “叶子”。

对于复杂的神经网络，也是如此。

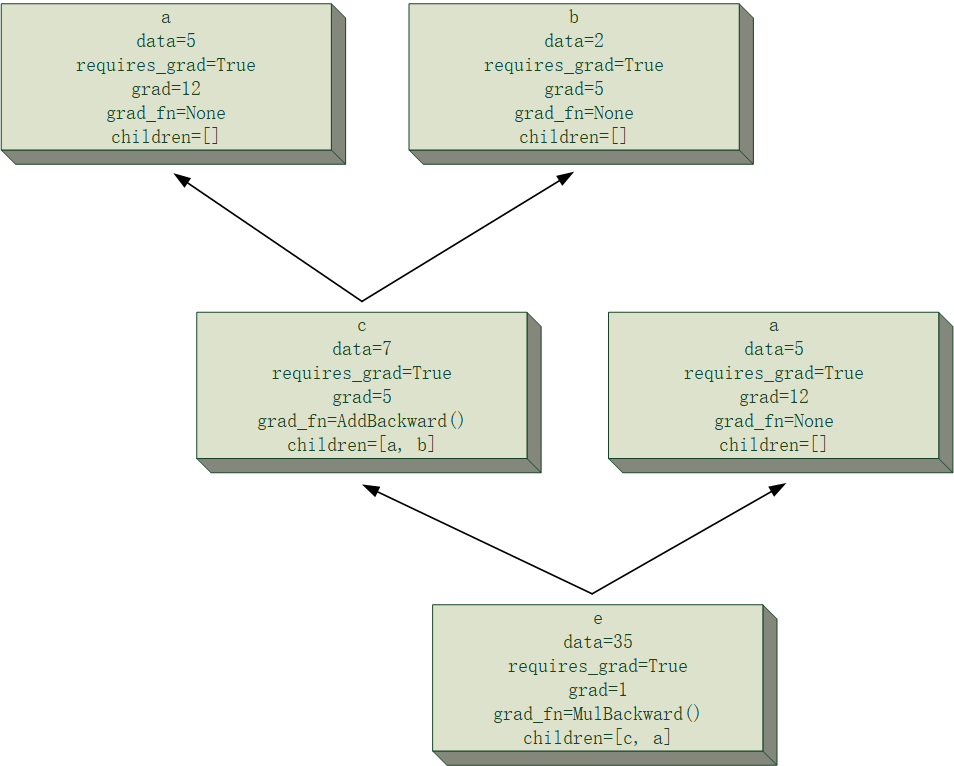
通过计算图，我们可以轻松地 “反其道而行”，得到误差对每一个叶子节点的梯度。

具体实现的时候，从根节点到叶子节点的路径很可能不止一条，例如以下这个例子：

$e = (x + y) \times x$ ，你可以自己试试将其画成计算图，然后试图用计算图的想法对 $x$ 计算梯度（其实就是让你巩固一下链式法则罢了）不要算的太快，记得把中间结果写出来。

上面这个式子对 $x$ 算梯度的时候，就有两条路径，分别是 $e \to (x + y) \to x$ 和 $e \to x$ ，对每一条路径，都可以计算一个对 $x$ 的偏导数出来，而最后 $e$ 对 $x$ 的梯度，则是把两部分进行求和，最后的结果便是 $2 \times x + y$ ，与直接口算的结果肯定是一样的。

从上面这个例子结合梯度的链式法则，可以看出，只要从根节点出发，深度优先遍历整个图，对叶子节点的每一次访问都相当于找到了一条梯度传播路径，将对某个叶子节点的所有路径上得到的偏导数进行求和，便得到对该叶子节点的梯度。另外，计算图的无环性也保证了路径不会进入循环，也就是说只要你沿着箭头的反方向走，就一定可以到达一片叶子，不会进入循环。以上就是通过计算图来计算叶子节点梯度的思路。

以上就是误差逆传播算法及计算图在此算法中起到的作用，若有不理解的，~~你上手写一下就理解了~~，欢迎来和我讨论。

计算图的构建方式

何为计算图的构建方式？说白了就是给你一个神经网络，你要通过什么方法把它的计算图搭出来。

计算图一旦能顺利搭出来，接下来就只需要处理各种运算的梯度就好了，困难也~~迎刃而解~~才走了不到五分之一（因为我发现各种运算的梯度计算才是最顶的 / 手动捂脸）。不过这样设计，耦合度瞬间降低了不少，只要为每种运算分别写一个梯度函数就好了。

但不论如何，这一步都是要做的，所以不妨先了解一下市面上都有哪些常用的构建方式。

计算图的构建方式主要有以 TensorFlow、Caffe 为代表的静态图以及以 PyTorch 为代表的动态图，二者的区别主要就体现在名字上。

动态图是指计算和图的构建过程同时进行的机制，通俗的讲，每计算一步，都会在已得到的图上增加一部分，计算至最终结果时，计算图即构建完成。这种方法每一步都能得到中间结果，更易于调试，而且实际写模型时，更容易把脑子里的 idea 转化为代码，编写效率更高。

静态图则与动态图不同，它是先将计算图定义好（包含正向传播和反向传播的运算流），在定义好计算图后，才开始正式计算。好处在于，计算图不需要多次构建，而是一次构建多次使用，运行效率理论上会更高（注意，是理论上，实际上科研人员并没有显著感觉 PyTorch 比 TensorFlow 慢多少）。但后果就是，较难及时拿到中间结果，调试难度更大，学习成本高。

其实我一开始写的时候并没有刻意想过究竟用哪种方式来构建计算图，而是直接用符合正常人思维的方式来写代码，写的差不多以后才发现，啊，原来这就是动态图。也是很灵性了。话又说回来，为什么 Google 在开发 TensorFlow 时会想到如此不符合正常人思维的静态图？大概是有其独到的想法吧。

神经网络中，张量是一切计算的核心，下一篇文章打算简单讲一下我用 Numpy 封装的张量类。