手搓神经网络系列之——梯度反传函数具体怎么写？（一）

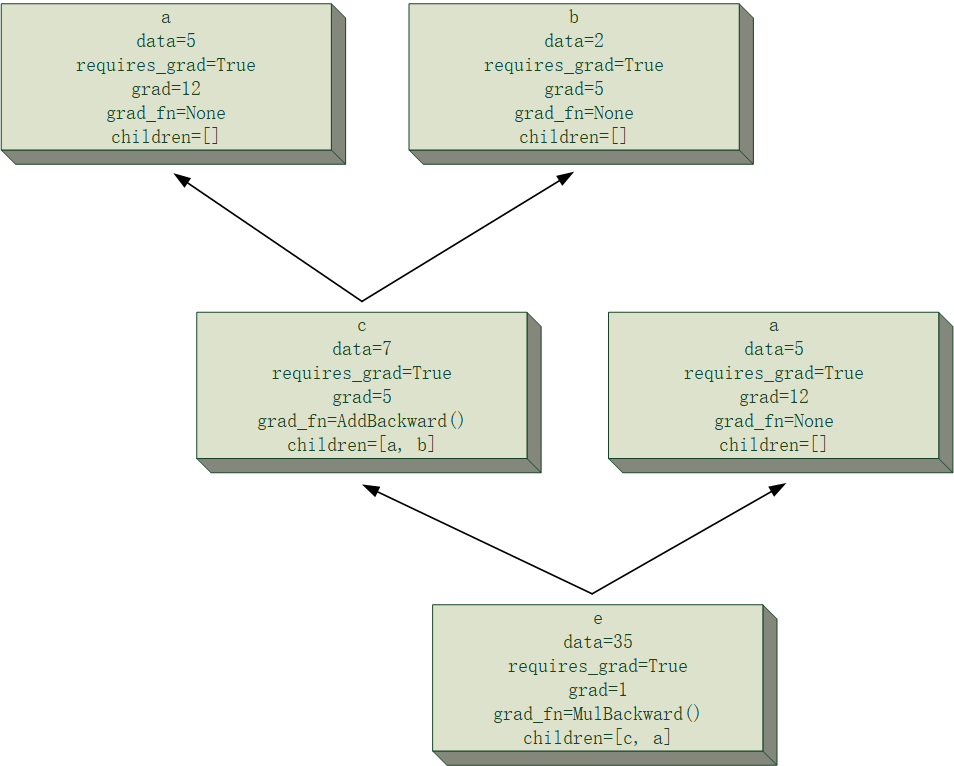
前一篇文章简单介绍了计算图的节点类（Tensor 类）的封装方法，在文末给了一个比较直观的反向传播模拟，我们发现，节点将梯度反传至其子节点的过程需要利用其梯度反传函数。

本系列全部代码见下面仓库：

autograd-with-numpy

GitHub

如有算法或实现方式上的问题，请各位大佬轻喷 + 指正！

为简单起见，在前面文章提到的例子里，所有节点的值均是一个标量，但在神经网络中，大部分节点都应该是矩阵或者更一般的张量形式，对张量运算计算梯度虽然原理类似，但仍会比标量复杂不少。而在代码实现时，其复杂程度的提升不仅仅来自于单变量到多变量的转变，还涉及到张量运算的广播机制。

对于神经网络里可能涉及到的梯度反传函数，我大概将其分为三类：

常见单变量函数的反传
常见矩阵（张量）运算的反传
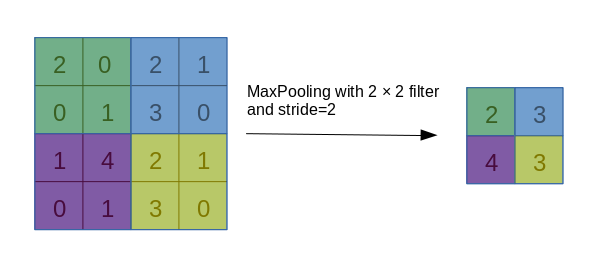
卷积、池化运算的反传

对于这三类我将从（我所认为的）简单到复杂，依次举一些我认为比较有代表性（简单）的例子。当然，限于篇幅，同样不可能面面俱到。但我认为，每一类里的思路是大体相同的。

单变量函数的梯度反传

常见单变量函数包含诸如指对数运算、Sigmoid、三角函数、绝对值函数（注意不是矩阵模）等，这些函数的特点是作用在单个张量上，即运算数只有一个，并且这类函数作用在一个张量上的效果，相当于函数对每一个元素进行单独作用，得到的结果形状与原张量相同。例如：

a b s ([\begin{matrix} 1 & - 2 & 3 \\ 2 & - 4 & 4 \end{matrix}]) = [\begin{matrix} 1 & 2 & 3 \\ 2 & 4 & 4 \end{matrix}]

对于这类函数，直接把单变量求导法则推广过去就可以了。例如对于绝对值函数的梯度反传函数我是这样考虑的：

对于 child 中每一个正值位，梯度传回系数为 1，对于 child 中每一个负值位，梯度传回系数为 - 1，对于 child 中值为 0 值位，梯度传回 0。

python

class AbsBackward(BackwardFcn):
    def calculate_grad(self, grad, children, place):
        x = children[0][0].data
        return (2. * (x >= 0.).astype(float) - 1.) * (x != 0) * grad

上面是我乱写的绝对值函数的梯度反传代码，注意到这个函数传入了三个参数：grad、children 与 place，在我的设计中，所有梯度反传函数均需要传入这三个参数，它们分别表示：

grad：当前节点的梯度
children：当前节点的所有子节点列表（计算梯度时很可能会需要其他子节点的信息，所以干脆把所有 children 传进去）
place：当前正在计算梯度的子节点在 children 中的位次（位次在非对称运算中挺重要的，例如减法运算，对两个运算数产生的梯度是不同的）

如上面绝对值运算的例子，若 $[\begin{matrix} 1 & 2 & 3 \\ 2 & 4 & 4 \end{matrix}]$ 的梯度为 $[\begin{matrix} a & b & c \\ d & e & f \end{matrix}]$ ，则传至 $[\begin{matrix} 1 & - 2 & 3 \\ 2 & - 4 & 4 \end{matrix}]$ 的梯度应该是 $[\begin{matrix} a & - b & c \\ d & - e & f \end{matrix}]$ 。如果你看不懂这是啥意思，那我建议你先去复习复习高中的导数。

与代码中的变量作个对应：

grad= $[\begin{matrix} a & b & c \\ d & e & f \end{matrix}]$ ，x= $[\begin{matrix} 1 & - 2 & 3 \\ 2 & - 4 & 4 \end{matrix}]$

这类单变量函数的梯度反传函数都比较容易写，于是我先把这部分实现了一下。

常见张量运算的梯度反传

张量运算包含最基本的 element-wise 加减乘除四则运算，其中，乘法除了 element-wise 乘法，还有张量的乘法，而后者又包含三种子情况，如下：

一维向量间点乘 ——Dot
多维张量与一维向量相乘 ——Mv
多维张量与多维张量相乘 ——Mm

另外，张量运算还包含一些特殊运算，例如转置运算、reshape 运算、最大最小值运算等，包含的内容之多，令人顿感头大，但若耐心地一条一条写，这些特殊运算梯度反传的思路其实并不难，总是能写完的。

限于篇幅，下文仅介绍张量 element-wise 四则运算的梯度反传思路。其余的留到后面文章再进行有选择性的讨论。

所谓 element-wise，即元素间的四则运算，在数学上，这种运算要求两个参与运算的张量具有相同的形状，如以下 element-wise Addition：

[\begin{matrix} 1 & 2 & 3 \\ - 1 & - 2 & - 3 \end{matrix}] + [\begin{matrix} 2 & 3 & 4 \\ - 1 & - 2 & - 1 \end{matrix}] = [\begin{matrix} 3 & 5 & 7 \\ - 2 & - 4 & - 4 \end{matrix}]

像上面这种形状相同的情况，不论是加减法还是乘除法，梯度反传其实都格外容易。以下以加法为例：

python

class AddBackward(BackwardFcn):
    def calculate_grad(self, grad, children, place):
        return grad

如果能确保加法运算中两个张量的形状相同，那么上面这样写就已经万无一失了。

然而，我们经常有对不同形状的张量进行元素间四则运算的需求。举个最常见的例子，将一个标量与一个 $2 \times 3$ 的矩阵相加，会得到什么？按数学的逻辑，这是会报错的行为，但显然 numpy 中是许可这类行为的，而且结果非常符合逻辑，它会把这个标量分别加到 $2 \times 3$ 矩阵的每一个元素上。

3 + [\begin{matrix} 1 & 2 & 3 \\ - 1 & - 2 & - 3 \end{matrix}] = [\begin{matrix} 4 & 5 & 6 \\ 2 & 1 & 0 \end{matrix}]

看似显然的结果，实则是张量运算中复杂的广播机制（Broadcast）的冰山一角。那么我们自然会想到一个问题：广播机制对梯度的反向传播有什么影响？

考虑以下计算式：

S u m (3 + [\begin{matrix} 1 & 2 & 3 \\ - 1 & - 2 & - 3 \end{matrix}]) = 18

请计算上式求和的结果 18 对 3 这个变量的梯度。

显然梯度不是 1 吧！因为广播机制的存在，3 这个变量相当于被加了 6 次，所以最后结果应该是 6 而不是 1。

那么这个 6 是从何而来？从这个例子里，很容易看出，6 恰好是这个被加矩阵的长宽之积，但这毕竟只是个最简单的例子，要想写出适应所有情况的代码，就免不了完全搞明白广播的运作机制。

广播机制（Broadcast）

菜鸟教程对广播的解释如下：

广播 (Broadcast) 是 numpy 对不同形状 (shape) 的数组进行数值计算的方式，对数组的算术运算通常在相应的元素上进行。
菜鸟教程

网上有不少广播机制的示意图，但我的目的是从逻辑上解释广播，故不再画图，直接总结一下广播机制的流程：

拿到两个张量后，可以通过下面的流程来判断这两个矩阵是否可以进行广播：

分别写出两个张量的形状，张量的形状是一个元组（tuple）类型的元素，特殊地，标量的形状为空元组。
若两个张量形状的长度不同（维数不同），对维数较小的张量，向前（元组的左侧方向）扩展大小为 1 的维度。
经过第 2 步的扩展，现在两个张量的维数已经相同，将两个张量当前的形状依维度进行比较。若遇到两个张量在某个维度上数值不同，并且两个张量在该维度上的长度均不为 1，则这两个张量无法进行广播。
否则，可以进行广播。对每一个张量，在所有大小为 1 的维度上，复制自身直至与另一个张量的该维度大小相同。

描述起来感觉有点晕乎，还是以具体的例子来说明吧，对于前面的例子：

3 + [\begin{matrix} 1 & 2 & 3 \\ - 1 & - 2 & - 3 \end{matrix}]

第一个张量，是个标量，于是形状为空元组：()；第二个张量，形状为 (2, 3)。
因为两个张量的维数不同，我们在维数较小的张量 (标量 3) 上，向前扩展长度为 1 的维度，直到两个张量维数相同。该操作结束后，标量 3 变成了二维矩阵 $[\begin{matrix} 3 \end{matrix}]$ ，形状变为了 (1, 1)。
依次比较 (1, 1) 和 (2, 3)，在两个张量第 0 个维度上，长度分别为 1 和 2，数值不同，但第一个张量在该维度上长度为 1，因此第 0 维通过；在第 1 个维度上，长度分别为 1 和 3，数值也不同，但第一个张量在该维度上长度同样是 1，因此第 1 维也通过。
因此，这两个张量能够进行广播，我们需要把第一个张量通过在第 0 维和第 1 维上复制自身的方式扩展到与第二个张量形状相同，因此，第一个张量又变成了：