手搓神经网络系列之 —— 卷积运算的反向传播（一）

前面写了整整三篇文章讨论了卷积运算的正向传播，本文将进入卷积运算的反向传播部分，将涉及到一些简单的数学公式推导（与其说是推导，不如说是瞪眼法 + 直接写结论），都是最简单的线性函数，不必裂开。

本系列全部代码见下面仓库：

autograd-with-numpy

GitHub

如有算法或实现方式上的问题，请各位大佬轻喷 + 指正！

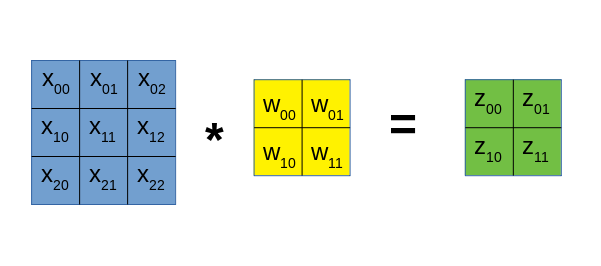
我们以下面简单的卷积过程为例，推导卷积运算的梯度传播式：

我们将上面的卷积过程展开写出来，得到下面 4 个方程：

已知传至张量 $Z$ 的梯度为 ${\delta }_Z$，我们分别对数据张量 $X$ 和卷积核张量 $W$ 计算梯度。

对 X 的梯度

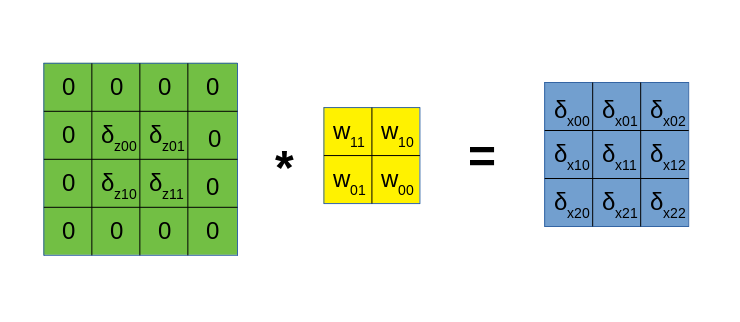
下面先计算对 $X$ 的梯度 ${\delta }_X$，通过简单的链式法则即可得到：

乍一看十分复杂，但事实上，通过瞪眼法我们可得出，这是以下卷积过程的展开式：

其中，左侧是 $Z$ 的梯度矩阵 ${\delta }_Z$ 经过一圈 padding 之后的样子，中间的卷积核是原来的卷积核 $W$，经过 180 度的旋转所得到的，回顾前一篇文章所讲到的，这种旋转相当于张量所有元素在内存上的顺序 reverse 了一下。

需要注意的是，若正向卷积时的步长大于 1，那么在这里计算梯度 ${\delta }_X$ 的时候，需要对梯度 ${\delta }_Z$ 额外进行一次插入 0 的操作，我将这种操作称为 dilate，各位可以自己去推导一下，看看究竟需要做什么操作。

我们可以将上面的梯度表达式简写为：

通过简单的推导，可以发现，pad 的圈数，应该与正向卷积的步长是相关的，不过其实还有一个巧妙的算法，即通过这三者的形状进行反推，感兴趣的话可以去推导一下。

对 W 的梯度

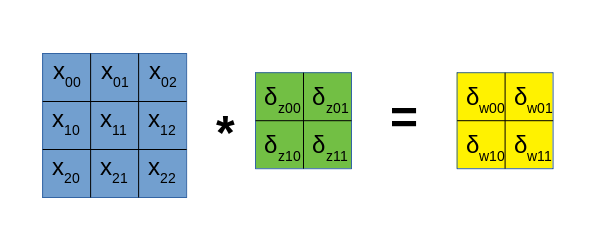
接下来计算对卷积核 $W$ 的梯度 ${\delta }_W$，同样由前面的方程进行链式法则计算：

这一组公式的规律更加明显了，其相当于下面的卷积运算的展开式：

与前面计算 ${\delta }_X$ 时类似，若正向卷积时的步长大于 1，那么在这里计算梯度 ${\delta }_W$ 的时候，同样需要对梯度 ${\delta }_Z$ 进行 dilate 操作，不过这里不需要 pad 0。

我们同样可以将上面的梯度表达式简写为：

以上，即是卷积运算的梯度传播公式，即便是高维情况下的卷积运算，也万变不离其宗。本文虽短，但思考为什么卷积的梯度传递会是这样的形式让我死了很多脑细胞。后面一篇文章，将进入卷积运算反向传播的代码实现部分！