手搓神经网络系列之——卷积运算的反向传播（二）

前一篇文章中我们简单推导了卷积运算的梯度传播公式，本文将通过代码实现卷积反向传播的过程。本文代码主要位于 nn/conv_operations.py 文件，反向传播代码位于 autograd/backward.py 文件。

本系列全部代码见下面仓库：

autograd-with-numpy

GitHub

如有算法或实现方式上的问题，请各位大佬轻喷 + 指正！

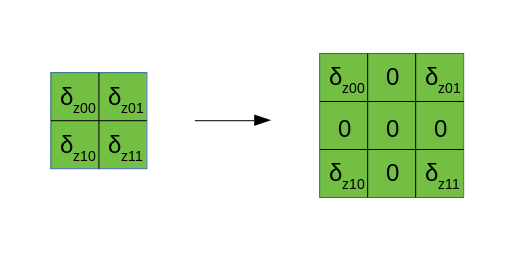
首先揭秘前面提到的 dilate 操作，在卷积步长 $S > 1$ 时，我们在对卷积核 $W$ 计算梯度 $δ_{W}$ 时，需要将 $δ_{Z}$ 进行所谓的 dilate 操作，下图为 $S = 2$ 时，需要进行的 dilate 操作示意图。

事实上，dilate 操作就是在相邻的行（列）之间插入一定行（列）数的 0，通过推导可以知道，每两行（列）之间插入 0 的行（列）数＝ $S - 1$ 。

另外，我们在反向传播的时候需要讨论一些额外的情况：数据的 padding 操作以及卷积核的 dilate 操作。相信用过 PyTorch 的朋友都知道，PyTorch 在卷积时，有一个 padding 参数和一个 dilation 参数，padding 一般来说是为了维持卷积前后数据的分辨率尺寸（长宽）不变，dilation 则是作用在卷积核上，是为了在参数量保持不变的情况下，增大卷积核的感受野。在做反向传播的时候，我们也要将 padding 和 dilation 这两种变换考虑进去（对于 padding，简单起见我们只考虑 pad 0 的情况），在使用了这两个变换的情况下，要用经变换后的数据、卷积核来进行梯度的计算，在得到计算结果后，再根据之前所做的变换，反变换回去。

几个基本函数

首先我们写几个经常会用到的函数，分别是 padding、dilate 以及它们的逆操作。

padding_zeros / unwrap_padding

python

def padding_zeros(x: np.ndarray, padding):
    """
    在张量周围填补0
    @param x: 需要被padding的张量,ndarray类型
    @param padding: 一个二元组,其每个元素也是一个二元组,分别表示竖直、水平方向需要padding的层数
    @return: padding的结果
    """
    if padding == ((0, 0), (0, 0)):
        return x
    n = x.ndim - 2
    x = np.pad(x, ((0, 0),) * n + padding, 'constant', constant_values=0)
    return x


def unwrap_padding(x: np.ndarray, padding):
    """
    padding的逆操作
    @param x:
    @param padding:
    @return:
    """
    if padding == ((0, 0), (0, 0)):
        return x
    p, q = padding
    if p == (0, 0):
        return x[..., :, q[0]:-q[1]]
    if q == (0, 0):
        return x[..., p[0]:-p[1], :]
    return x[..., p[0]:-p[1], q[0]:-q[1]]

dilate / erode

python

def dilate(x: np.ndarray, dilation=(0, 0)):
    """
    膨胀,在各行、列间插入一定数量的0
    """
    if dilation == (0, 0):
        return x
    *bc, h, w = x.shape
    y = np.zeros((*bc, (h - 1) * (dilation[0] + 1) + 1, (w - 1) * (dilation[1] + 1) + 1), dtype=np.float32)
    y[..., ::dilation[0] + 1, ::dilation[1] + 1] = x
    return y


def erode(x: np.ndarray, dilation=(0, 0)):
    """
    腐蚀,与膨胀互为逆运算
    """
    if dilation == (0, 0):
        return x
    y = x[..., ::dilation[0] + 1, ::dilation[1] + 1]
    return y

上面的代码相对比较容易理解，而且并非本文重点，故不再解释。需要注意的是，所有上面的运算，都只作用在数据的分辨率维度上（长宽所在维度）。

另外，我们还需要一个运算，即前面文章提到过的 rotate180 操作：

python

def rotate180(kernel: np.ndarray, axis=(-1, -2)):
    return np.flip(kernel, axis)

我使用了 np.flip 函数来完成这个操作。

卷积的正向传播

接下来就到了卷积反向传播的硬核内容了，首先我们给出正向传播代码：

python

def conv2d(x: Tensor, weight: Tensor, bias: Tensor = None, stride=(1, 1), padding=(0, 0), dilation=(0, 0)):
    assert x.ndim == 4, 'x must be 4 dimensional'
    b, c, h, w = x.shape
    oc, ic, kh, kw = weight.shape
    assert c == ic, 'Conv2d channels not equal'
    stride = _pair(stride)
    padding = _pair(padding)
    dilation = _pair(dilation)
    padding = ((padding[0], padding[0]), (padding[1], padding[1]))
    padded_data = padding_zeros(x.data, padding)
    dilated_weight = dilate(weight.data, dilation)
    split = split_by_strides(padded_data, dilated_weight.shape[-2:], stride=stride)
    output = Tensor(np.tensordot(split, dilated_weight, axes=[(1, 4, 5), (1, 2, 3)]).transpose((0, 3, 1, 2)),
                    requires_grad=x.requires_grad)
    if bias is not None:
        output = output + bias[:, None, None]
    if output.grad_enable:
        output.children = [(x, padded_data, padding), (weight, dilated_weight, stride, dilation)]
        if bias is not None:
            output.children.append((bias, None))
        output.grad_fn = Conv2dBackward()
    return output

前面未曾讨论卷积正向传播中的 bias，但个人认为它比较容易处理，就是一个带广播的加法操作罢了。上面的代码，核心部分是从 padded_data = padding_zeros(x.data, padding) 开始的，下面给出核心代码的解释：

padded_data = padding_zeros(x.data, padding)，对数据进行 padding 操作。
dilated_weight = dilate(weight.data, dilation)，对卷积核进行 dilate 操作。
split = split_by_strides(padded_data, dilated_weight.shape[-2:], stride=stride)，熟悉的 split_by_strides，将数据进行分割。
output = Tensor(np.tensordot(split, dilated_weight, axes=[(1, 4, 5), (1, 2, 3)]).transpose((0, 3, 1, 2)), requires_grad=x.requires_grad)，得到卷积结果，封装成计算图节点数据类型 Tensor。

在得到卷积结果后，我们再处理 bias 的部分：

python

if bias is not None:
    output = output + bias[:, None, None]

最后再指定 children 和 grad_fn：

python

if output.grad_enable:
    output.children = [(x, padded_data, padding), (weight, dilated_weight, stride, dilation)]
    if bias is not None:
        output.children.append((bias, None))
    output.grad_fn = Conv2dBackward()

在 children 中，我们记录的信息比较多且杂，其中与 x 放在一起的有经过 padding 之后的数据 padded_data 和 padding 参数值，与 weight 放在一起的有经过膨胀操作的卷积核 dilated_weight，卷积的步长 stride，以及膨胀尺寸 dilation。放这么多内容的原因除了提供必要的参数外，还有为了在反向传播时尽量避免重复操作。

卷积的反向传播

下面我们给出反向传播代码：

python

class Conv2dBackward(BackwardFcn):
    def calculate_grad(self, grad, children, place):
        x, padding = children[0][1:]
        if place == 0:
            dilated_weight, stride = children[1][1: 3]
            grad = dilate(grad, (stride[0] - 1, stride[1] - 1))
            delta_x_shape = x.shape[-2] + sum(padding[0]), x.shape[-1] + sum(padding[1])
            add_rows, add_cols = np.array(delta_x_shape) + dilated_weight.shape[-2:] - 1 - np.array(grad.shape[-2:])
            padding_x = np.floor(add_rows / 2).astype(int), np.ceil(add_rows / 2).astype(int)
            padding_y = np.floor(add_cols / 2).astype(int), np.ceil(add_cols / 2).astype(int)
            grad = padding_zeros(grad, (padding_x, padding_y))
            return unwrap_padding(reverse_conv2d(grad, dilated_weight, rotate=True, invert=False), padding)
        elif place == 1:
            x = padding_zeros(x.data, padding)
            stride, dilation = children[1][2:]
            grad = dilate(grad, (stride[0] - 1, stride[1] - 1))
            return erode(reverse_conv2d(x, grad, rotate=False, invert=True), dilation)
        else:
            return np.sum(grad, (0, -1, -2))

我们将其分成三个部分来分别解读，三个部分分别计算了 $δ_{X}$ ， $δ_{W}$ 和 $δ_{B}$ （bias 的梯度）。

$δ_{X} = p a d (d i l a t e (δ_{Z})) * r o t a t e 180 (W)$

python

dilated_weight, stride = children[1][1: 3]
grad = dilate(grad, (stride[0] - 1, stride[1] - 1))
delta_x_shape = x.shape[-2:]
add_rows, add_cols = np.array(delta_x_shape) + dilated_weight.shape[-2:] - 1 - np.array(grad.shape[-2:])
padding_x = np.floor(add_rows / 2).astype(int), np.ceil(add_rows / 2).astype(int)
padding_y = np.floor(add_cols / 2).astype(int), np.ceil(add_cols / 2).astype(int)
grad = padding_zeros(grad, (padding_x, padding_y))
return unwrap_padding(reverse_conv2d(grad, dilated_weight, rotate=True, invert=False), padding)

代码中的 grad 相当于公式中的 $δ_{Z}$ ，首先根据公式，我们将 grad 进行 dilate 和 padding 操作，dilate 插入 0 的行列数是步长减去 1，而 padding 增加的行列数：padding_x、padding_y，则是我通过形状反向算出来的，只是一点简单的形状推导，如果你懒得推，我在后面给了一个例子。

最后我们带着变换后的 $δ_{Z}$ 和卷积核，进入一个被我称为 reverse_conv2d（反向卷积）的函数，其实这个函数就是做了一个普通的卷积运算，只是额外加了一些操作，例如卷积核的 rotate180。注意，如果在卷积过程中给了卷积核膨胀参数，那么最后传入的卷积核，是经过膨胀后的卷积核，这是因为我们这里计算的是对数据矩阵 $X$ 的梯度。

下面给出 reverse_conv2d 函数：

python

def reverse_conv2d(x: np.ndarray, kernel: np.ndarray, rotate=False, invert=False):
    """
    conv2d的反向卷积,求梯度时用的
    @param x: 被卷积的张量
    @param kernel: 卷积核
    @param rotate: 卷积核旋转180度
    @param invert: 该参数有点迷,不好解释,简单的说就是反向卷积有两种,视卷积结果的形状需要调整一些轴的位置
    @return: 反向卷积结果
    """
    ksize = kernel.shape
    x = split_by_strides(x, ksize[-2:])
    if rotate:
        kernel = rotate180(kernel)
    i = 0 if invert else 1
    y = np.tensordot(x, kernel, [(i, 4, 5), (0, 2, 3)])
    if invert:
        return y.transpose((3, 0, 1, 2))
    return y.transpose((0, 3, 1, 2))

注意到，这其实就是一个普通的卷积运算，区别在于，首先我们判断了是否要对卷积核进行 rotate180 操作，另有一个相对比较难理解的参数 ——invert，这个参数说白了其实是用来调整轴的位置的，下面我们根据一个实际的例子，来形象地说明为什么需要这个参数。

考虑下面一个步长为 1、数据不进行 padding、卷积核不做 dilate 的卷积： $X * W = Z$

$(8, 3, 4, 4) * (6, 3, 2, 2) = (8, 6, 3, 3)$

我们计算 $δ_{X}$ ，根据公式，我们需要将 $δ_{Z}$ 进行 padding、dilate 后与 rotate 后的卷积核进行卷积。我们首先知道，grad ( $δ_{Z}$ ) 的形状应该是 (8, 6, 3, 3)，卷积核的形状是 (6, 3, 2, 2)，它俩卷积要得到 (8, 3, 4, 4) 的形状（即 $δ_{X}$ 的形状），那么需要把 (8, 6, 3, 3) 增大到 (8, 6, 5, 5)，也就是 padding 一圈，因此，进入 reverse_conv2d 函数的 grad，形状为 (8, 6, 5, 5)，dilated_weight 形状为 (6, 3, 2, 2)，在 reverse_conv2d 函数中，通过 split_by_strides 得到的 x 的形状自然是 (8, 6, 4, 4, 2, 2)，与前面的卷积类似，它将与 dilated_weight 进行 tensordot 运算，我们可以直接根据形状，来判断需要指定哪些轴作为求和轴，两者的形状分别是 (8, 6, 4, 4, 2, 2) 与 (6, 3, 2, 2)，那么这种情况下，求和轴应该是 [(1, 4, 5), (0, 2, 3)]，在代码中对应的即是 invert 参数为 False 的情况。tensordot 得到的张量形状为 (8, 4, 4, 3)，而我们期望得到的形状是 (8, 3, 4, 4)，因此我们再做一个 transpose((0, 3, 1, 2)) 的操作，将原来的 3 轴换到 1 轴的位置上。基于类似的考虑，可以发现在计算 grad( $δ_{W}$ ) 时，需要将 invert 参数置为 True。

还记得前面卷积正向传播的时候，指定的求和轴是哪些吗 ——[(1, 4, 5), (1, 2, 3)]，而这里是 [(1, 4, 5), (0, 2, 3)]，为什么卷积核的求和轴，从 (1, 2, 3) 变成了 (0, 2, 3)？除了从形状必须一一对应这个角度解释外，从另一个角度，因为这里是计算对 $X$ 的梯度，在卷积运算时，每一个卷积核都会分别与 $X$ 进行作用，因此在反向传播梯度的时候，每一个卷积核都会拥有与 $X$ 的梯度相关的部分，在最后就需要对它们进行求和，这也是求和轴包含了卷积核的 Out_Channels 维度的原因。

我们继续回到反向传播的最后一句代码：

python

return unwrap_padding(reverse_conv2d(grad, dilated_weight, rotate=True, invert=False), padding)

从 reverse_conv2d 函数出来后，我们需要将结果反 padding 一下，原因是我们计算得到的结果，实际上是对 padding 后的 $X$ 的梯度，因此真正的 $δ_{X}$ ，还需要把结果去掉周围的 padding。

$δ_{W} = X * d i l a t e (δ_{Z})$

python

x = padding_zeros(x.data, padding)
stride, dilation = children[1][2:]
grad = dilate(grad, (stride[0] - 1, stride[1] - 1))
return erode(reverse_conv2d(x, grad, rotate=False, invert=True), dilation)

这段代码用以计算对卷积核的梯度 $δ_{W}$ ，在实际运用公式时，如果正向卷积使用了 padding，那么公式中的 $X$ 也是经过 padding 后的 $X$ 。

所以第一步我们把 x 进行 padding，接下来同样地，我们根据公式，把 grad（ $δ_{Z}$ ）进行 dilate，并塞入 reverse_conv2d 函数，这个公式里，我们不需要把卷积核 rotate180，因此指定 rotate 参数为 False，另一个参数 invert，这里指定为 True。这一次，你可以试试判断一下在这种情况下，tensordot 求和轴是哪些以及最后的 transpose 应该如何换轴。

最后，如果在卷积正向传播中，卷积核经过了 dilate，那么我们求出来的卷积核梯度，其实也是 dilate 以后的梯度，故我们在最后需要 erode 一下，把它还原回去。

$δ_{B}$

python

return np.sum(grad, (0, -1, -2))

计算 bias 的梯度 $δ_{B}$ ，只有一句代码，十分简单，建议各位自己在纸上推导一下，看看为什么是这样算的。

本文将卷积运算的反向传播过程通过代码进行了实现，将卷积的反向传播过程从公式转化为代码有一点困难（至少对我而言），希望各位可以仔细研究，写出自己的卷积反向传播代码。

完成了二维卷积后，对于一维卷积（序列卷积），我们只需将其扩展为 H=1、对应步长为 1 的二维卷积情形：

python

def conv1d(x: Tensor, weight: Tensor, bias: Tensor = None, stride=1, padding=0, dilation=0):
    assert x.ndim == 3, 'x must be 3 dimensional'
    return conv2d(x.unsqueeze(-2), weight.unsqueeze(-2), bias, (1, stride), (0, padding), (0, dilation)).squeeze(-2)