手搓神经网络系列之——池化与BN层

结束了本系列最硬核的卷积反向传播部分，从这篇文章开始，将进入比较软核的内容，本文来介绍池化运算和 BN 层的正反向传播。

本文涉及到的数学公式比较多，网页前端渲染会比较慢，烦请耐心等待和阅读。

本系列全部代码见下面仓库：

引用站外地址，不保证站点的可用性和安全性

autograd-with-numpy

GitHub

如有算法或实现方式上的问题，请各位大佬轻喷 + 指正！

池化

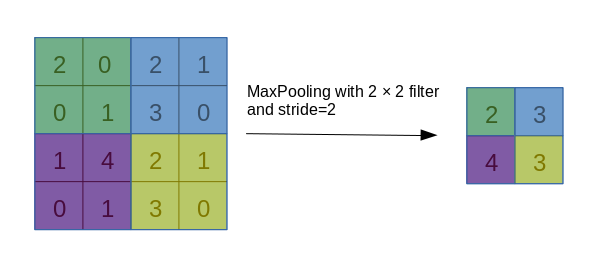
池化运算（Pooling），是一种对数据的采样方式，通过减小数据的分辨率尺寸来加速运算，其本质是信息完整性与运算速度的妥协。最常用的池化操作即最大池化（MaxPooling），过程如下图所示：

一般而言，以上面这种池化核尺寸为 2、步长为 2 的池化操作最为常用。还有一种平均值池化，则是把每一块的最大值运算换成平均值运算。

前向传播

池化与卷积很像，因此前向传播时，我们可以利用前面卷积时用到的 split_by_strides 函数，以下给出 MaxPooling 的前向传播：

python

def max_pool2d(x: Tensor, kernel_size, stride=None):
    assert x.ndim == 4, 'x must be 4 dimensional'
    kernel_size = _pair(kernel_size)
    stride = stride or kernel_size
    stride = _pair(stride)
    split = split_by_strides(x.data, kernel_size, stride)
    max_data = np.max(split, axis=(-1, -2))
    argmax = np.argmax(split.reshape(-1, kernel_size[0] * kernel_size[1]), axis=-1).flatten()
    output = Tensor(max_data, requires_grad=x.requires_grad)
    if output.grad_enable:
        output.children = [(x, argmax, kernel_size, stride)]
        output.grad_fn = MaxPool2dBackward()
    return output

与卷积类似，我们通过 split_by_strides 函数就可以直接把数据按块分割出来，然后对最后两个维度进行取最大值运算即可。

反向传播

反向传播的思路也很简单，与前面的 Max 运算的思想是一样的，区别在于若遇到存在多个最大值的情况，只为第一个最大值传回梯度，其余的则传回 0。

我直接用循环解决了：

python

class MaxPool2dBackward(BackwardFcn):
    def calculate_grad(self, grad, children, place):
        x, argmax, kernel_size, stride = children[0]
        new_grad = np.zeros_like(x.data)
        B, C, H, W = grad.shape
        for index, m in zip(product(range(B), range(C), range(H), range(W)), argmax):
            b, c, h, w = index
            mh, mw = m // kernel_size[1], m % kernel_size[1]
            new_grad[b, c, h * stride[0] + mh, w * stride[1] + mw] += grad[b, c, h, w]
        return new_grad

说来惭愧，我用循环的原因是目前没有想到更好的适应一切情况的方法，不过，池化的反向传播因为不涉及到矩阵运算，所以感觉用循环也没事，不怎么影响运行效率。

这里的代码都非常容易理解，我就不再解读了（其实是因为太不优雅了而不想解读）。

AvgPooling 和 MaxPooling 类似，这里不再贴代码。

BN 层

BN 层，全称 Batch Normalization 层，作用是稳定数据分布、加速训练，经常被用在神经网络的激活函数之前。

BN 层的正向传播分为训练阶段和测试阶段两种情况。

在训练阶段，BN 层需要收集数据的一些统计信息，BN 层在拿到每一批次的数据后，首先要计算出这批数据每一个通道的均值、方差，拿到均值和方差后，BN 层通过滑动的方式动态更新自己的 running_mean 和 running_var 属性，即滑动均值和滑动方差，最后，用计算出来的均值、方差对数据的每一个通道进行标准化：

{\hat{x}}^{(k)} = \frac{x^{(k)} - μ^{(k)}}{σ^{(k)}}, k = 1, 2, \dots, C

但若就这么结束了，将会带来很大的问题，因为数据在被标准化之后，前面所有层学习到的特征也会被破坏，因此 BN 层还引入了两个可训练参数 $γ, β$ ，在把数据归一化以后，又做了一个 affine 变换：

y^{(k)} = γ^{(k)} {\hat{x}}^{(k)} + β^{(k)}, k = 1, 2, \dots, C

$y$ ，即是 BN 层最后的输出结果。

在测试阶段，BN 层使用训练时收集到的 running_mean 和 running_var 对数据进行归一化，使用训练时学习到的 $γ$ 与 $β$ 进行 affine 变换。

数学推导

根据以下传播公式，我们给出 BN 层反向传播的梯度推导。

μ = \frac{1}{n} \sum_{i = 1}^{n} x_{i}, σ = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (x_{i} - μ)^{2}}

{\hat{x}}_{i} = \frac{x_{i} - μ}{σ}

y_{i} = γ \hat{x_{i}} + β

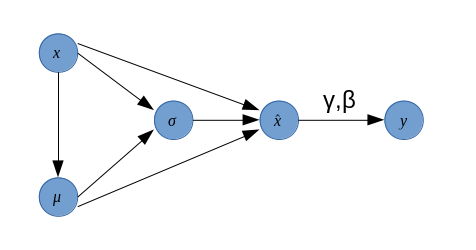
下面来计算梯度，为清晰起见，我们先画出上述式子的计算图：

我们首先对 $γ, β$ 计算梯度，这两个比较容易：

δ_{γ} = \sum_{i = 1}^{n} \hat{x_{i}} δ_{y_{i}}, δ_{β} = \sum_{i = 1}^{n} δ_{y_{i}}

然后作为跳板，我们计算 $δ_{\hat{x}}$ ：

δ_{\hat{x}} = γ δ_{y}

接下来计算最复杂的 $δ_{x}$ ，我们将其分为三条梯度链，用链式法则来解决：

δ_{x_{i}} = δ_{{\hat{x}}_{i}} \frac{\partial {\hat{x}}_{i}}{\partial x_{i}} + δ_{μ} \frac{\partial μ}{\partial x_{i}} + δ_{σ} \frac{\partial σ}{\partial x_{i}}

目前 $δ_{x_{i}}$ 已经得到，我们还需计算的梯度有 $\frac{\partial {\hat{x}}_{i}}{\partial x_{i}}, δ_{μ}, \frac{\partial μ}{\partial x_{i}}, δ_{σ}, \frac{\partial σ}{\partial x_{i}}$ ，下面来依次计算：

$\frac{\partial {\hat{x}}_{i}}{\partial x_{i}}$

根据 ${\hat{x}}_{i} = \frac{x_{i} - μ}{σ}$ ，容易得出：

\frac{\partial {\hat{x}}_{i}}{\partial x_{i}} = \frac{1}{σ}

$δ_{μ}$

δ_{μ} = \sum_{i = 1}^{n} δ_{{\hat{x}}_{i}} \frac{\partial {\hat{x}}_{i}}{\partial μ} + δ_{σ} \frac{\partial σ}{\partial μ}

易知 $\frac{\partial σ}{\partial μ} = 0$ ，故：

\begin{aligned} δ_{μ} & = \sum_{i = 1}^{n} δ_{{\hat{x}}_{i}} \frac{\partial {\hat{x}}_{i}}{\partial μ} \\ = - \frac{1}{σ} \sum_{i = 1}^{n} δ_{{\hat{x}}_{i}} \end{aligned}

$\frac{\partial μ}{\partial x_{i}}$

\frac{\partial μ}{\partial x_{i}} = \frac{1}{n}

$δ_{σ}$

由 ${\hat{x}}_{i} = \frac{x_{i} - μ}{σ}$ ，得到：

δ_{σ} = - \frac{1}{σ^{2}} \sum_{i = 1}^{n} δ_{{\hat{x}}_{i}} (x_{i} - μ)

$\frac{\partial σ}{\partial x_{i}}$

由 $σ = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (x_{i} - μ)^{2}}$ ，得到：

\frac{\partial σ}{\partial x_{i}} = \frac{x_{i} - μ}{n σ}

现在，所有的梯度都已经算出来了，我们将它们代回原式，通过一些化简，可以求出 $δ_{x_{i}}$ ：

\begin{aligned} δ_{x_{i}} & = δ_{{\hat{x}}_{i}} \frac{\partial {\hat{x}}_{i}}{\partial x_{i}} + δ_{μ} \frac{\partial μ}{\partial x_{i}} + δ_{σ} \frac{\partial σ}{\partial x_{i}} \\ = \frac{δ_{{\hat{x}}_{i}}}{σ} - \frac{1}{n σ} \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} - \frac{x_{i} - μ}{n σ^{3}} \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} (x_{j} - μ) \\ = \frac{1}{n σ} (n δ_{{\hat{x}}_{i}} - \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} - \frac{x_{i} - μ}{σ} \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} \frac{x_{j} - μ}{σ}) \\ = \frac{1}{n σ} (n δ_{{\hat{x}}_{i}} - \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} - {\hat{x}}_{i} \sum_{j = 1}^{n} δ_{{\hat{x}}_{j}} {\hat{x}}_{j}) \end{aligned}

代码

最后，给出 BN 层正反向传播的代码：

正向传播

python

def forward(self, x: Tensor)
    axis = (0, -1, -2)[:x.ndim - 1]
    if self.training:
        batch_mean = Tensor(np.mean(x.data, axis=axis, keepdims=True))
        batch_var = Tensor(np.var(x.data, axis=axis, keepdims=True))
        if self.track_running_stats:
            self.running_mean = (1. - self.momentum) * self.running_mean + self.momentum * batch_mean
            self.running_var = (1. - self.momentum) * self.running_var + self.momentum * batch_var
        return F.batch_norm(x, batch_mean, batch_var, self.gamma, self.beta, self.eps)
    if self.track_running_stats:
        return F.batch_norm(x, self.running_mean, self.running_var, self.gamma, self.beta, self.eps)
    batch_mean = Tensor(np.mean(x.data, axis=axis, keepdims=True))
    batch_var = Tensor(np.var(x.data, axis=axis, keepdims=True))
    return F.batch_norm(x, batch_mean, batch_var, self.gamma, self.beta, self.eps)

首先，根据输入数据 x 的维数（3 或 4），确定计算均值和方差时用到的 axis（相当于去掉了 Channel 所在的 1 轴），接下来的操作分为 training 阶段或 eval 阶段，具体过程前面已经讲过了，这里省略一千字，直接来到最后调用的 batch_norm 函数。

python

def batch_norm(x: Tensor, mean: Tensor, var: Tensor, gamma: Tensor, beta: Tensor, eps=1e-5):
    axis = (0, -1, -2)[:x.ndim - 1]
    x_hat = (x.data - mean.data) / np.sqrt(var.data + eps)
    output = Tensor(np.expand_dims(gamma.data, axis) * x_hat + np.expand_dims(beta.data, axis), requires_grad=x.requires_grad or gamma.requires_grad or beta.requires_grad)
    if output.grad_enable:
        output.grad_fn = BatchNormBackward()
        output.children = [(x, x_hat, mean.data, var.data, eps), (gamma, None), (beta, None)]
    return output

batch_norm 函数也没啥好讲的，就是老老实实按前面的公式进行计算得到 $y$ 即可，唯一需要注意的是 gamma、beta 在这里没办法直接 broadcast（它俩的形状都是 (C,)，而 x_hat 的形状则是 (B, C, H, W) 或 (B, C, L)，因此需要手动扩展维度再进行 affine 运算）。

在计算图的 children 中，也额外放了一些信息，分别对应前面公式里的 $\hat{x}, μ, σ^{2}$ ，以便于梯度的计算。

接下来是反向传播代码：

python

class BatchNormBackward(BackwardFcn):
    def calculate_grad(self, grad, children, place):
        x, x_hat, mean, var, eps = children[0]
        axis = (0, -1, -2)[:x.ndim - 1]
        gamma = children[1][0]
        grad_x_hat = grad * np.expand_dims(gamma.data, axis)
        if place == 0:
            n = grad.size / grad.shape[1]
            dx = n * grad_x_hat - np.sum(grad_x_hat, axis=axis, keepdims=True) - \
                x_hat * np.sum(x_hat * grad_x_hat, axis=axis, keepdims=True)
            dx = dx / (n * np.sqrt(var + eps))
            return dx
        elif place == 1:
            return np.sum(x_hat * grad, axis=axis)
        else:
            return np.sum(grad, axis=axis)

由于梯度的公式已经明明白白地写在了前面，这里的反向传播代码基本没啥可说的了，只要注意一下不要搞错维度就行。

可能有朋友会问，我们不是已经实现了这些基本运算的梯度传播了嘛，为什么还要大费周章地进行人力求导呢？这是因为我们计算了梯度之后发现，x 的梯度可以利用很多已经得到的信息（如 x_hat）进行快速计算，把这个计算图的反向传播过程打包成一个 BatchNormBackward，在运算效率上有一定的提升，这样的例子还有不少，例如我前面已经提过一次的交叉熵损失函数。

本文虽然不算硬核，但涉及到的数学公式推导相对于前面的卷积更复杂些，希望诸位能自己在纸上从头至尾推导一遍，这块内容只要能把公式推出来，代码只是水到渠成。

如果对池化的反向传播有更好的建议，麻烦告诉我！

至此，计算图、反向传播部分已经实现的差不多了（其实反向传播还有一堆没写 hhh，但不重要，这些只是时间问题罢了），后面的文章将完善模型的优化部分，最后将尝试通过自己写的神经网络来训练一个简单的模型。